This PLECS demo model shows a two-axle electric vehicle model with front-wheel drive and simulated driving profiles for both mechanical and regenerative braking modes. The effect on the vehicle speed and weight distribution due to various torque commands can be observed.
System Model
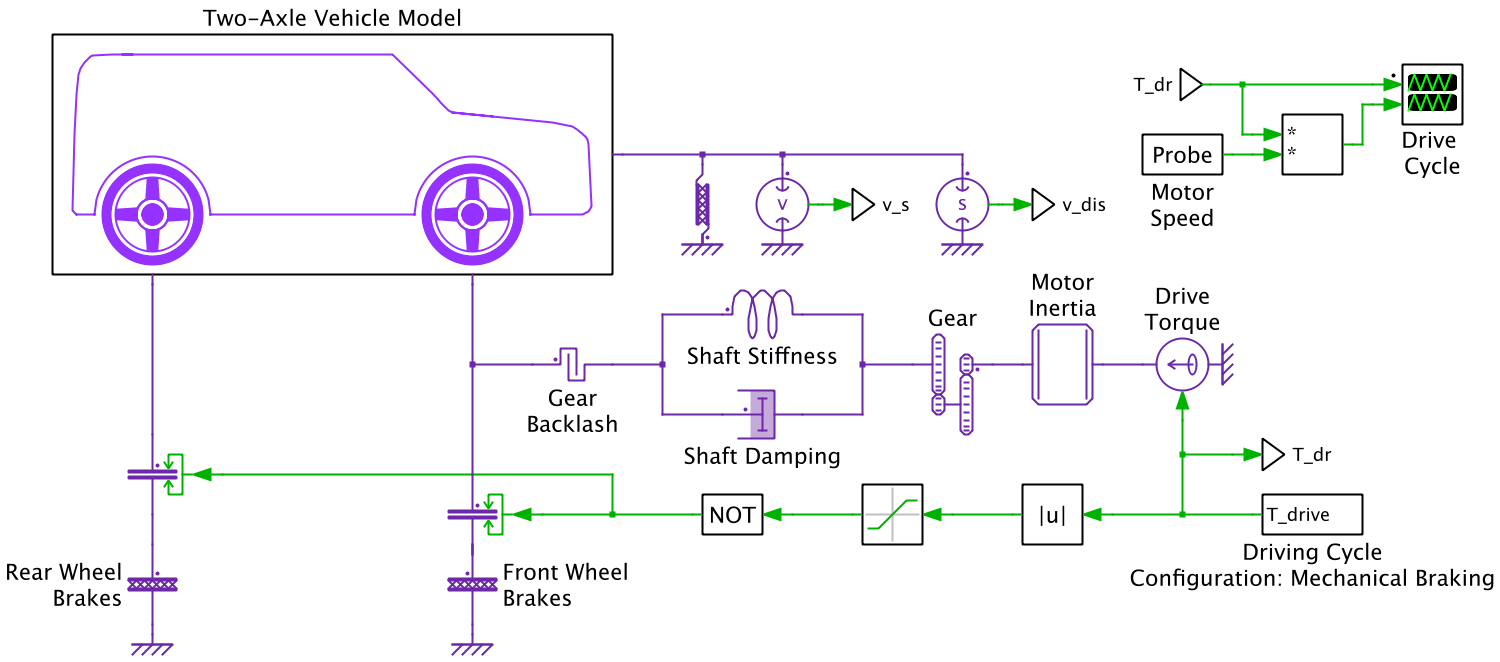
The electric motor is connected to the front-wheel axle of the two-axle vehicle model. An ideal torque source is used to apply the motor torque on the rotor, modeled here as a rotating body of fixed inertia. The rotor shaft is then connected to the wheel axle through a gearbox. The shaft stiffness and damping are modeled using a torsion spring and a rotational damper, respectively.
The total traction force generated by both the front and rear wheels is then applied to the vehicle, represented here as a lumped mass. Rotational friction blocks are used to model the front and rear wheel brakes. The vehicle model converts the applied torque on the wheel axle into a traction force applied on the vehicle using a slip-based wheel model. In addition, the vehicle is connected to a road load.
Vehicle Model
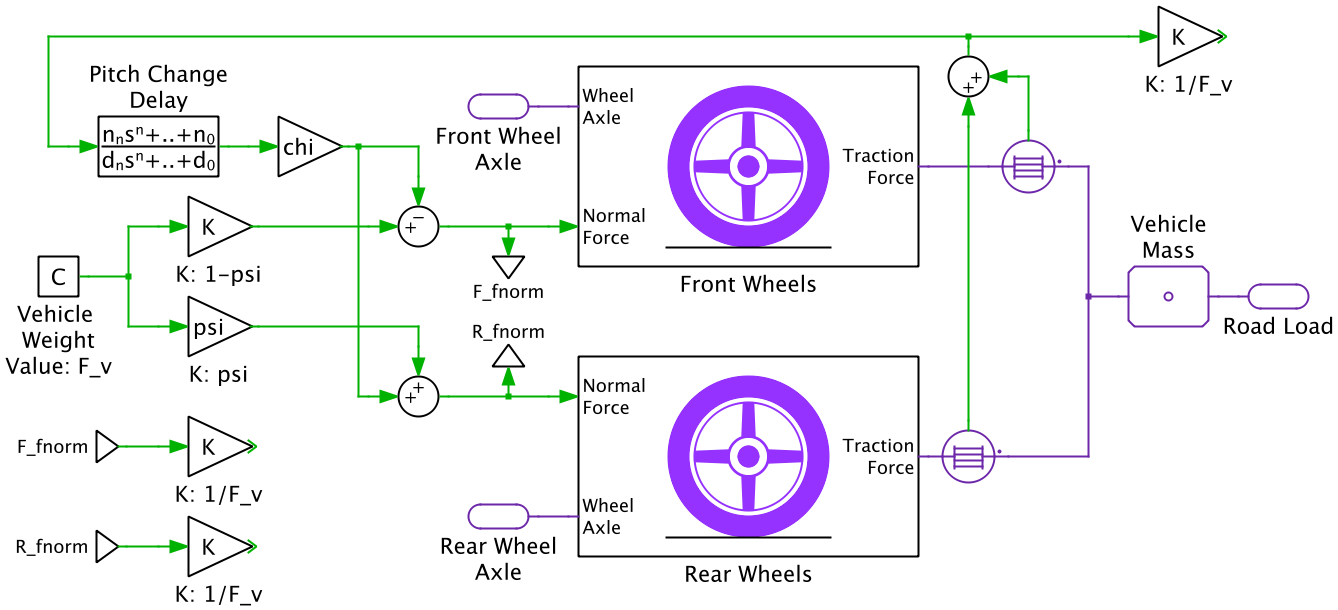
The weight on the front and rear axle is distributed according to the location of the center of gravity. In this example, the center of gravity is assumed to be closer to the front wheel axle to model a front-engine vehicle. The wheel model converts the torque applied on the wheel axle into a traction force. The total traction force generated by both the front and rear wheels is then applied to the vehicle represented here as a lumped mass. The vehicle model also incorporates the effect of acceleration/deceleration on the weight distribution of the vehicle. The “Pitch Change Delay” is used to model the stiffness of the vehicle suspension system.
Wheel Model
The torque applied to the axle acts on a wheel, which is modeled in a lumped fashion as a rotational inertia block. The rotational speed of the wheel as well as the translational speed of the vehicle (vs) are both measured. The rotational speed of the wheel is scaled by the radius of the wheel to determine the translational speed of the tire (vw) near the point of contact with the road. The normal force acting on the wheel axle and the measured speeds (vw and vs) are used to calculate the traction force (Ft) applied to the vehicle by the wheels. The applied traction force will then move the total vehicular system.
There are two implementations for the calculation of the tire slip. A "Basic Tire Model" ignores the transient behavior of the tires while the "Restricted Fully Nonlinear Model" incorporates the transient behavior of the tire/wheel, resulting in a wind-up oscillation when a step change in torque is applied to the wheel.
Simulation
Driving Profile
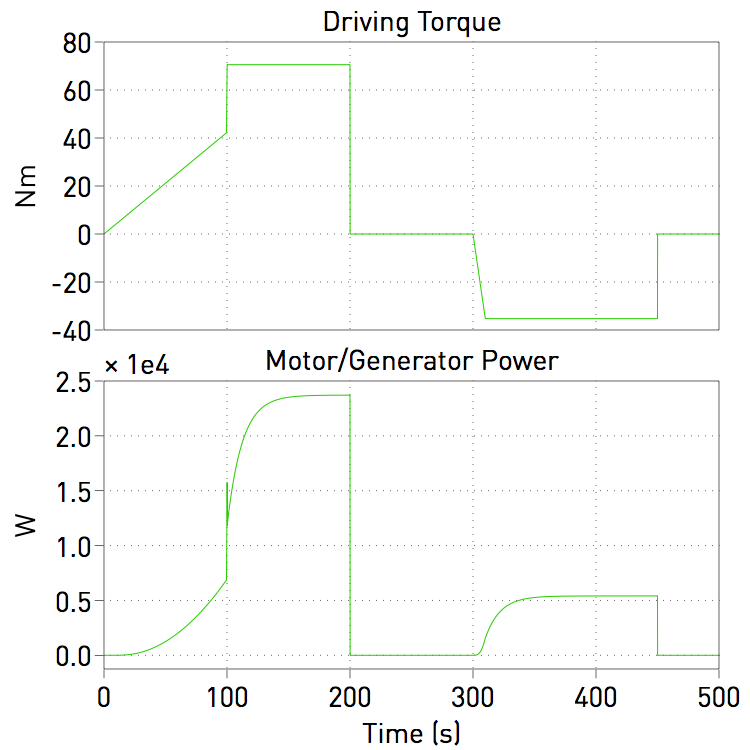
The figure above shows the torque applied by the electric motor on the vehicular system over the length of the simulation. A ramped accelerating torque demand is applied on the motor for the first 100 seconds. At t=100 seconds, the vehicle is suddenly accelerated leading to a step change in the torque applied by the electric machine. At t=200 seconds, the driver uses the mechanical brakes to slow the vehicle, leading to zero torque being applied by the motor. At t=300 seconds, a negative torque is applied by the motor to reverse the vehicle. This torque is maintained over the next 150 seconds when the mechanical brakes are employed again to bring the vehicle to a standstill. Additionally, the power required by the motor is also plotted. As can be seen, the electric machine is only operated in motoring mode in this drive cycle. The effect of the simulated drive cycle on the velocity and weight distribution of this vehicle is easily observed.
Regenerative Braking
An alternative to decelerating the vehicle with mechanical braking is to use the generation capabilities of the electric machine to recapture the kinetic energy, hence slowing the vehicle. A second driving cycle that includes this feature is also provided with the model.
Try it
This model is available in the PLECS Demo Model library provided in both versions of PLECS.
